PENGERTIAN TURUNAN DAN SIFAT-SIFATNYA


 Nama : Mila dwi andini (26)

Kelas : XI IPS 3


Turunan merupakan suatu perhitungan terhadap perubahan nilai fungsi karena perubahan nilai input (variabel).

Turunan dapat disebut juga sebagai diferensial dan proses dalam menentukan turunan suatu fungsi disebut sebagai diferensiasi.

Menggunakan konsep limit yang sudah dipelajari, turunan dapat didefinisikan sebagai

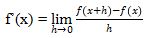
Rumus Turunan

turunan tersebut didefinisikan sebagai limit dari perubahan rata-rata dari nilai fungsi terhadap variabel x.

Selanjutnya akan dijelaskan mengenai contoh penerapan turunan.


SIFAT-SIFAT TURUNAN

  1. Aturan Konstanta

    Jika f(x) = k dengan k suatu konstanta maka untuk sebarang x, f'(x) = 0 yakni Dx(k) = 0

  2. Aturan Fungsi Identitas
    Jika f(x) = x maka f'(x) = 1 yakni Dx(x) = 1

  3. Aturan Pangkat

    Jika f(x) = xn, dengan n bilangan-bilangan bulat positif maka f(x) = nxn-1 yakni Dx(xn) = nxn-1

  4. Aturan Kelipatan Konstan

    Jika k suatu konstanta dan f suatu fungsi yang terdiferensial maka (kf)’ = k f'(x) yakni Dx[k f(x)] = k Dx[f(x)]

  5. Aturan Jumlah

    Jika f dan g fungsi-fungsi yang terdiferensial maka (f + g)(x) = f(x) + g(x) yakni Dx[f(x) + g(x)] = Dx[f(x)] + Dx[g(x)]

  6. Aturan Selisih

    Jika f dan g fungsi-fungsi yang terdiferensial maka (f – g)(x) = f(x) – g(x) yakni Dx[f(x) – g(x)] = Dx[f(x)] – Dx[g(x)]

  7. Aturan Hasil Kali

    Jika f dan g fungsi-fungsi yang terdiferensial maka (f . g)'(x) = f'(x)g(x) + f(x)g'(x) yakni Dx[f(x)g(x)] = Dx[f(x)]g(x) + f(x)Dx[g(x)]

  8. Aturan Hasil Bagi

    Jika f dan g fungsi-fungsi yang terdiferensial maka \left ( \frac{f}{g} \right )(x)= \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)} yakni Dx \frac{f(x)}{g(x)}= \frac{D_x[f(x)]g(x)-f(x)D_x[g(x)]}{g^2(x)}


CONTOH SOAL

Contoh soal 1
Diketahui , nilai dari f’(5) adalah ...

a.    6
b.    10
c.    14
d.    17
e.    20

Pembahasan :

    f’(x) = 2x + 4
    f’(5) = 2(5) + 4
            = 14
JAWABAN: C


Contoh soal 2
Turunan pertama dari   adalah ...
Pembahasan :


JAWABAN: D


Contoh soal 3
Diketahui  dan f’ adalah turunan pertama dari f. Nilai dari f’(1) = ...
a.    20
b.    21
c.    23
d.    23
e.    26
Pembahasan :


               = 24 – 6 + 6 – 1
               = 23
JAWABAN: C


Contoh soal 4
Diketahui  dan f’ adalah turunan pertama f. Nilai f’(1) adalah ...
a.    3
b.    8
c.    13
d.    16
e.    21
Pembahasan :


              = 3 – 20 + 25
              = 8
JAWABAN: B


Contoh soal 5
Diketahui . Jika f’ adalah turunan pertama dari f, maka nilai f’(x) = ...
Pembahasan :
Kita gunakan rumus ini ya: 


JAWABAN: D


Contoh soal 6
Jika dengan f’ adalah turunan pertama f, maka nilai f’(2) adalah ...
a.    5
b.    20
c.    30
d.    40
e.    50
Pembahasan :
Kita gunakan rumus ini ya: 


               = 20.1
               = 20
JAWABAN: B


Contoh soal 7
Jika f(x) = sin x cos 3x maka f’(π/6) = ...
Pembahasan :
f(x) = sin x cos 3x
      = ½ (sin 4x + sin (-2x))
      = ½ sin 4x – ½ sin 2x
f’(x) = ½ . 4 cos 4x – ½ . 2 cos 2x
        = 2cos 4x – cos 2x
Maka:
f’(π/6) = 2cos 4(π/6) – cos 2(π/6)
           = 2.(- ½ ) – ½
           = -1 – ½
           = -1 1/2
JAWABAN: C


Contoh soal 8
Jika  , sin x ≠ 0 dan f’ adalah turunan f, maka f’(π/2) = ...
a.    -2
b.    -1
c.    0
d.    1
e.    2
Pembahasan :

Misalkan: u = sin x + cos x --> u’ = cos x – sin x
    v = sin x --> v’ = cos x
Ingat rumus ini ya: 
Sehingga:


JAWABAN: B


Contoh soal 9
Nilai maksimum dari fungsi  adalah ...
a.    8
b.    12
c.    16
d.    24
e.    32
Pembahasan :
Nilai maksimum atau minimum suatu fungsi diperoleh jika f’(x) = 0
Maka:


Jadi, nilai maksimumnya adalah 12
JAWABAN: B


Contoh soal 10
Turunan fungsi  adalah ...
Pembahasan :
 atau 
Maka:

JAWABAN: B


Contoh soal 11
 Diketahui fungsi dan turunan pertama dari f adalah f’. Maka f’(x) = ...
a.    4 sin (2x + 3) cos (2x + 3)
b.    -2 sin (2x + 3) cos (2x + 3)
c.    2 sin (2x + 3) cos (2x + 3)
d.    -4 sin (2x + 3) cos (2x + 3)
e.    sin (2x + 3) cos (2x + 3)
Pembahasan :

    f’(x) = 2 sin (2x + 3) . 2. cos (2x + 3)
           = 4sin(2x + 3)cos(2x + 3)
JAWABAN: A


Contoh soal 12
Grafik fungsi  turun dalam interval ...
a.    x < -3 atau x > 1
b.    x < -1 atau x > 3
c.    x < -3 atau x > -1
d.    -1 < x < 3
e.    1 < x < 3
Pembahasan :
Syarat grafik f(x) turun adalah jika nilai f’(x) < 0, maka:


    HP = -1 < x < 3
JAWABAN: D


Contoh soal 13
Turunan pertama fungsi  adalah f’(x). Nilai f’(1) = ...
a.    18
b.    24
c.    54
d.    162
e.    216
Pembahasan :

Misalkan: 
               v = 2x – 1 -->  v’ = 2
Kita pakai rumus yang ini: f(x) = u.v --> f’(x) = u’.v + u.v’
Sehingga:

             = 18 . 9 . 1 + 27 . 2
             = 162 + 54
             = 216
JAWABAN: E


Contoh soal 14
Suatu proyek akan diselesaikan dalam x hari. Jika biaya proyek per hari adalah dalam ribuan rupiah maka biaya proyek minimum dalam x hari sama dengan ...
a.    Rp550.000,00
b.    Rp800.000,00
c.    Rp880.000,00
d.    Rp900.000,00
e.    Rp950.000,00
Pembahasan :
 atau 
Biaya minimum diperoleh ketika B’(x) = 0
B’(x) = 4x – 40
B’(x) = 0
4x – 40 = 0
4x = 40
x = 10
Subtitusikan x = 10 dalam persamaan 
Jadi, biaya proyek minimum dalam x hari sama dengan Rp800.000,00
JAWABAN: B


Contoh soal 15
Untuk memproduksi suatu barang diperlukan biaya produksi yang dinyatakan dengan fungsi  dalam ribuan rupiah. Agar biaya minimum maka harus diproduksi barang sebanyak ...
a.    30
b.    45
c.    60
d.    90
e.    135
Pembahasan :

Agar biaya minimum maka B’(x) = 0
B’(x) = 4x – 180
B’(x) = 0
4x – 180 = 0
4x = 180
x = 45
Jadi, agar biaya minimum maka harus diproduksi barang sebanyak 45
JAWABAN: B



DAFTAR PUSTAKA :
  • https://rumuspintar.com/turunan/
  • https://aimprof08.wordpress.com/2012/05/02/turunan-dan-sifat-sifatnya/
  • https://www.ajarhitung.com/2017/02/contoh-soal-dan-pembahasan-tentang_14.html

Komentar

Posting Komentar

Postingan populer dari blog ini

SOAL CERITA DENGAN PENYELESAIANNYA GUNAKAN INVERS DAN DETERMINAN MATRIKS

Gambar
SOAL CERITA DENGAN PENYELESAIANNYA MENGGUNAKAN INVERS DAN MATRIKS Nama : MILA DWI ANDINI (26) Kelas: XI IPS 3 1. Arman membeli 5 pensil dan 3 penghapus, sedangkan Susi membeli 4 pensil dan 2 penghapus di toko yang sama. Di kasir, Arman membayar Rp 11.500,00 sedangkan Susi membayar Rp 9.000,00. Jika Dodi membeli 6 pensil dan 5 penghapus, berapa ia harus membayar?  Persoalan ini dapat diselesaikan menggunakan dua cara. Jika   maka dengan  cara pertama , yakni cara invers, diperoleh   . determinan dari   adalah ad - bc. Penyelesaian cara kedua adalah cara determinan, yaitu: Penyelesaian  Dimisalkan harga satuan pensil = x dan harga satuan penghapus = y. Disusun ke dalam sistim persamaan linear dua variabel (SPLDV) 5x + 3y = 11.500 4x + 2y = 9.000 Sistim persamaan di atas dapat dinyatakan dalam bentuk matriks, yakni Cara Pertama (Invers Matriks)           dan  Diperoleh harga satuan pensil Rp 2.000 dan harga sat...
Baca selengkapnya

PERTUMBUHAN, BUNGA TUNGGAL, BUNGA MAJEMUK, BUNGA ANUITAS, PELURUH DAN BEBERAPA CONTOH SOAL

Gambar
 Nama : Mila dwi andini (26)  Kelas : XI IPS 3 Bunga Tunggal, Bunga Majemuk, Penyusutan, & Anuitas Perhitungan untuk bunga, penyusutan, pertumbuhan, dan peluruhan  mengunakan konsep baris dan deret pada aritmatika dan geometri. Sehingga sebelum mempelajari ini, terlebih dahulu mempelajari konsep  barisan dan deret . Baris aritmatika merupakan baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui penjumlahan atau pengurangan dengan suatu bilangan b. Sedangkan, deret aritmatika merupakan penjumlahan suku-suku dari suatu barisan aritmatika. Baris geometri merupakan baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui perkalian dengan suatu bilangan r. Sedangkan, deret geometri adalah penjumlahan suku-suku dari suatu barisan geometri. Bunga Bunga (suku bunga) atau bank interest adalah pertambahan jumlah modal yang diberikan oleh bank untuk para nasabahnya dengan dihitung dari presentase modal uang nas...
Baca selengkapnya

TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI, DENGAN MATRIKS

Gambar
  TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI, DENGAN MATRIKS Nama: Mila dwi andini (26) Kelas: XI IPS 3 Translasi Translasi atau pergeseran adalah suatu transformasi yang memindahkan tiap titik pada bidang dengan jarak dan arah tertentuk.  Secara pemetaan dapat dituliskan: T =  ( a b )  : P(x,y) → P'(x+a , y+b) Titik P' disebut bayangan titik P oleh translasi T =  ( a b ) Contoh Soal 1 Tentukan bayangan titik (3,-7) oleh translasi   ( 4 2 ) Pembahasan: Misalkan titik P(3,-7). T =  ( 4 2 )  : P(3,-7) → P'(3+4 , -7+2) = P'(7,-5) Jadi, bayangan titik (3,-7) oleh translasi   ( 4 2 )  adalah (7,-5) Contoh Soal 2 Diketahui koordinat titik P adalah (4,-1). Oleh karena translasi  ( 2 a )  diperoleh bayangan titik P yaitu P'(-2a, -4). Tentukanlah nilai a. Pembahasan: T =  ( 2 a )  : P(4,-1) → P'(-2a , -4)   P'(-2a, -4) = P'(2+4, a+(-1)) P'(-2a, -4) = P'(6, (a-1)) ⟺-2a = 6 ⟺ a = 6/-2 ⟺ a = -3 Jadi, n...
Baca selengkapnya